Uvod do programovani v 3D

ÚVOD DO PROGRAMOVÁNÍ V 3D

Obsah

Úvod
Vysvětlení základních pojmů
Transformace vertexu
2D projekce vertexu
Polygon a plane
Ořezávání
Vykreslování

ZBuffer
Painter's Algorithm
SpanBuffer
BSP

Textury

Affiní
Perspektivní

Úvod

V tomto dokumentu najdete základní informace o tom co je třeba vědět pro základy programování v 3D. Budu používat vžité anglické výrazy pro
pojmenovávání pojmů. Dále budu používat programovací jazyk C pro příklady funkcí. Pro pochopení tohoto dokumentu je nutná alespoň základní
znalost a orientace ve 2D.

Vysvětlení základních pojmů

Vertex je bod nebo vrchol v 3D prostoru definován třemi souřadnicemi X,Y,Z. Osa X jde pravo, osa Y skrz obrazovku a osa Z jde nahoru. Viz obr.1.
Polygon je plocha o třech nebo výce vertexech. Viz obr.2.
Face je polygon o třech vrcholech. Je to nejjednodušší plocha v prostoru.. Viz obr.3.
Plane je plocha která je definována pouze postavením v prostoru a vzdáleností od počátku souřadnicového systému. Viz obr.4.
Vektor je veličina která udává velikost a směr. Např. pohyb loďky v řece. Viz obr.5.
Kamera je vlastně bod ze kterého se díváme do view space. Je definována jedním vertexem a třemi úhly.
FOV (Field of View). FOV je úhel kterým definujeme perspektivitu 2D promítání kamery. Viz obr. 6.
World Space je prostor který je počítan od počátku souřadnicového systému (0,0,0). Je to vlastně model ve kterém jsou uloženy polygony.
View Space je transformovaný world space. Jde o posunutí souřadnic a otočení o úhly které definuje kamera. Čili otočení ve směru pohledu.
Screen Space je 2D prostor na obrazovce monitoru. Z view space se transtormuje pomocí perspektivního promítaní do 2D.
Matice je třírozměrné pole pro rotace a posuvy v prostoru.

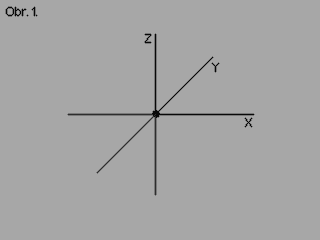
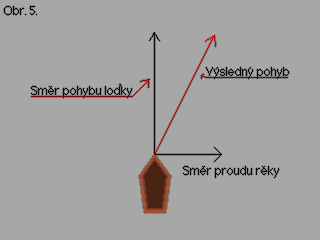
Transformace vertexu

vertex

world space

view space

Struktura vertexu je následující. typedef struct { float x,y,z} vertex_t;

#define ushort    usnsigned short; // Všechny úhly jsou uloženy v typu short protože nám to zaručí automatické přetočení z 360 na 0 a naopak.
                                                   // 180° = 32768 , 90° = 16384
// Definujeme matici.
float view_matrix[3][3];
// Kamera
camera_t cam;
^{////////////////////////////////////////}
^{void rotateMatrix_X(float *out,ushort a)}
^{////////////////////////////////////////}
^{
^{float s = sin(a * MPI / 0x8000);}
^{float c = cos(a * MPI / 0x8000);}
^{float y,z;}
^{y = c * out[1] + s * out[2];}
^{z = -s * out[1] + c * out[2];}
^{out[1] = y;}
^{out[2] = z;}
^}

^{////////////////////////////////////////}
^{void rotateMatrix_Y(float *out,ushort a)}
^{////////////////////////////////////////}
^{
^{float s = sin(a * MPI / 0x8000);}
^{float c = cos(a * MPI / 0x8000);}
^{float x,z;}
^{z = c * out[2] + s * out[0];}
^{x = -s * out[2] + c * out[0];}
^{out[0] = x;}
^{out[2] = z;}
^}

^{////////////////////////////////////////}
^{void rotateMatrix_Z(float *out,ushort a)}
^{////////////////////////////////////////}
^{
^{float s = sin(a * MPI / 0x8000);}
^{float c = cos(a * MPI / 0x8000);}
^{float x,y;}
^{x = c * out[0] + s * out[1];}
^{y = -s * out[0] + c * out[1];}
^{out[0] = x;}
^{out[1] = y;}
^}

^{/////////////////////////////////////////}
^{void setUpViewMatrix(float *m,angle_t *a)}
^{/////////////////////////////////////////}
^{
^{rotateMatrix_Y(m,a->ty);}
^{rotateMatrix_X(m,a->tx);}
^{rotateMatrix_Z(m,a->tz);}
^}

^{///////////////////////////}
^{void initMatrix(void)}
^{//////////////////////////}
^{
^{// vytvoření matice 1,0,0}
^{//
0,1,0}
^{//
0,0,1}
^{memset(&view_matrix,0,sizeof(float) * 9);}
^{view_matrix[0][0] = view_matrix[1][1] = view_matrix[2][2]
= 1;}
^{setUpViewMatrix(view_matrix[0],&cam->angle);}
^{setUpViewMatrix(view_matrix[1],&cam->angle);}
^{setUpViewMatrix(view_matrix[2],&cam->angle);}
^}

Nyní jsme vytvořili matici potřebnou pro rotaci vertexů. Tato matice se vytváří pouze na začátku každého snímku nebo při změně pohledu kamery.

Nyní každý potřebný vertex posuneme a zrotujeme pomocí následujícíího vzorce.Použijeme k tomu vzorce DOT_PRODUCT.

float dot(vector_t *v1,vector_t *v2)
{
    return(v1->x * v2->x +
                v1->y * v2->y +
                v1->z * v2->z);
}

V.X = vertex.x - camera.x
V.Y = vertex.y - camera.y
V.Z = vertex.z - camera.z

// Pozor zde musíme prohodit osu Y a Z.
X = Dot(&V,&view_matrix[0]);
Y = Dot(&V,&view_matrix[2]);
Z = Dot(&V,&view_matrix[1]);

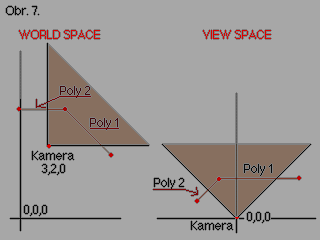
Teď máme vertex transformovám z world space do view space s tím že osa Y a Z se navzájem prohodí. Ale nemusíme to dělat, protože tady jde
jen o pojmenování. Nyní nám osy X a Y jdou stejně jako souřadnice obrazovky stím že osa Y jde směrem nahoru a osa Z skrz obrazovku.

2D projekce vertexu

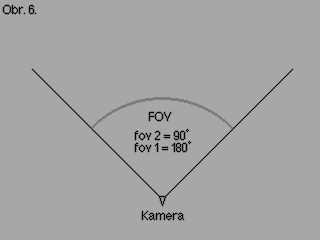
Teď musíme 3D vertex promítnout na 2D obrazovku do screen space. Předem musíme nastavit FOV na potřebnou hodnotu. Nejčastěji na (2.00).
Naším cílem je získat dvě souřadnice (SX,SY).
Následující proměná 'inv = 1 / Z' je tu kvůly rychlosti. Protože jinam bychom musely provádět 2 dělení což je pomalejší než 1 dělení a 2 násobení.
inv = 1 / 10; // 0.1
x = 5 * inv; // 0.5
y = 8 * inv; // 0.8
Je stejné jako
x = 5 / 10; // 0.5
y = 8 / 10; // 0.8

Čili jakmile dělíme 2 nebo výce čísel stejným dělitelem použijte inverzní operaci.

// xcenter a ycenter je středed obrazovky.
// scrx,scry je rozzlišení obrazovky
float inv = 1 / Z; // Nyní jde osa Z skrz obrazovku a osa Y jde nahoru.
SX = X * inv * (scrx / FOV) + xcenter;
SY = -Y * inv * (scry / FOV) + ycenter; // Musíme dát osu Y zápornou aby nám šla od zhora dolů.

Dalšího zrychlení dosáhneme započítaním (scrx / FOV) a (scry / FOV) do matice následujícím způsobem.
view_matrix[0] *= (scrx / FOV);
view_matrix[2] *= (scry / FOV);
Ovšem pro každý sloupec matice.

Polygon a Plane

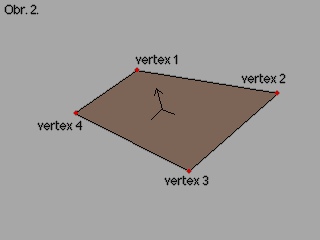
    Polygon je definován sadou vertexů kde směr následujícího vertexu jde většinou ve směru hodinových ručiček.Viz obr. 2.
Toto nám zaručí to že víme ze kreré strany polygon vidíme. Pomocí plane to zjistíme následujícím vzorcem.

if (dot((vector_t *)&plane.normal,&camera_pos) - plane.distance < 0) return; // V tomto případě polygon vidíme z druhé strany
                                                                                                                                //   a není ho třeba kreslit.
    Struktura plane je následující : typedef struct { float normal[3]; float distance;} plane_t;
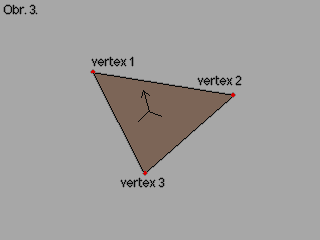
Normála nám definuje orientaci polygonu v prostoru. Je to číslo v rozmezí (-1 .. +1). Normála je kolmá k polygonu viz obr. 2. a 3. Je to vlastně
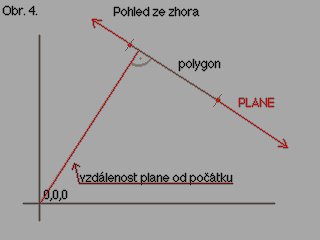
vektor který směřuje k počátku souřadnicového systému. Distance plane je nejkratčí vzdálenost normaly polygonu od počátku souřadnicové soustavy. Viz obr. 4. Například plane (0,0,1,0) nám říká že polygon leží k ose X svisle k ose Y také a k ose Z leží kolmo směrem nahoru
vzdálen o (0). To znamená že polygon leží jako podlaha. Plane (0,0,-1,10) leží jako strop ve vzdálenosti (10). Jinak řečeno 1 je kolma a 0 je svislá.
Struktura polygonu může být následující typedef struct {int numverts; vertex_t pts[4]; plane_t plane} polygon_t;
Tady je funkce na výpočet plane vzaná z GRAPHIC GEMS.

/////////////////////////////////////////////////
void calcPolyPlane(face_t *polygon)
/////////////////////////////////////////////////
{
float           len;
int             i;
vector_t        ref, normal;
vector_t        *v1, *v2;
ref.x = ref.y = ref.z = 0.0;
normal.x = normal.y = normal.z = 0.0;
   for(i=0; i<polygon->numverts; i++)
     {
        v1 = &polygon->pts[i];
        v2 = &polygon->pts[(i + 1) % polygon->numverts];
        normal.x += (v1->y - v2->y)*(v1->z + v2->z);
        normal.y += (v1->z - v2->z)*(v1->x + v2->x);
        normal.z += (v1->x - v2->x)*(v1->y + v2->y);
        ref.x += v1->x;
        ref.y += v1->y;
        ref.z += v1->z;
     }
   // Vektorová délka je sqrt(x*x + y*y + z*z)
   len = ml_vectorlength(&normal);
   polygon->plane.normal.v[0] = normal.x / len;
   polygon->plane.normal.v[1] = normal.y / len;
   polygon->plane.normal.v[2] = normal.z / len;
   len *= polygon->numverts;
   polygon->plane.distance = dot(&ref, &normal) / len;
}

Ořezávání

Někdy dodělám.

Frostware Home Page
https://members.tripod.com/~frostware/